(C) 2003 Hank Wallace
The code exhibited in this article has been adapted and flown on the UKube-1 satellite! For more information on the UKube-1, see this article.
This is the scene: Smoke wafts slowly in the darkened room, as with a mind of its own. Seedy characters sit at a dirty table under a naked bulb. At the focus, a Ouija board. Surrounding are piles of paper — data stacked upon data upon data, casting stark shadows. A sheet is snatched, examined, a scribble and it’s back to the pile. Occult bookies hard at work? No, error correction!
Well, that was my vision of it, until I was forced to bone-up for a recent communications project. I found out that error correction is not really like what you see in the movies, smoky mirrors, crystal balls, and evil mathematicians. If your vision of error correction is something to be avoided, I would like to help you change that image.
Most engineers are familiar with basic methods to verify the integrity of data transmitted over noisy communications channels. Simple checksums and cyclic redundancy checks (CRCs) are the most popular. Presented here is a related coding technique by which errors can not only be detected, but removed from received data without retransmissions.
This code bears the name of its discoverer, Marcel J. E. Golay. The first reference to his work is a note he published in a 1949 Bell technical journal1. Then, there was much activity in information coding techniques spurred by Claude Shannon’s 1948 landmark work, The Mathematical Theory Of Communication. The codes that Golay discovered can enhance the reliability of communication on a noisy data link.
Before we proceed, a note of caution. The theory of error detection and correction is deep (but not necessarily dark), as you can verify from any of the references cited. This article is intended only to give a brief overview of one of the many codes available. We will not dwell on the mathematical details or terse comparisons error correction techniques. If your system design calls for error correction methods, the C program fragments here may help you evaluate the Golay code. Just keep in mind that this is not a theoretically thorough treatment of this almost bottomless, fascinating subject. For that, see the references, and be sure you have a fresh pot of coffee on hand because you’re going to need it!
We should get a couple of simple definitions out of the way to make what follows easier to digest.
Weight: The count of bits which are ones in a binary word. For example, the weight of the byte 01011011 is five since it contains five 1s.
Hamming Distance: The number of bits which differ between two binary numbers. If A and B are binary numbers, the distance is weight(A XOR B). For example, the Hamming distance between bytes 4Ah and 68h is weight(4Ah XOR 6Fh) = weight(22h) = 2 bits.
Forward Error Correction: A technique which can correct errors at the receiver without relying on retransmissions of data.
Codeword Structure
Let’s jump right in and examine the structure of the binary Golay code. A codeword is formed by taking 12 information bits and appending 11 check bits which are derived from a modulo-2 division, as with the CRC.
| Check bits | Information bits |
|---|---|
| XXX XXXX XXXX | XXXX XXXX XXXX |
We will examine the modulo-2 division process later. The common notation for this structure is Golay [23,12], indicating that the code has 23 total bits, 12 information bits, and 23- 12=11 check bits. Since each codeword is 23 bits long, there are 223, or 8,388,608 possible binary values. However, since each of the 12-bit information fields has only one corresponding set of 11 check bits, there are only 212, or 4096, valid Golay codewords. You can think of the codewords as being distributed sparsely along the number line.
The Golay codewords are not really spread evenly as you count along the number line, say every few ticks. Rather they are spaced with regard to the Hamming distance between them. It turns out that each Golay codeword has seven or more bits differing from every other. Mathematicians say that the code has a minimum distance, d, of seven. They have determined analytically that the Golay code can detect and correct a maximum of (d-1)/2=3 bit errors, in any pattern.
To augment the power of the Golay code, an overall parity bit is usually added, resulting in a clean three-byte codeword called the extended Golay code, noted as Golay [24,12]. With this parity bit, all odd numbers of bit errors can be detected in each codeword, as well as all 4-bit errors.
| Parity bit | Check bits | Information bits |
|---|---|---|
| X | XXX XXXX XXXX | XXXX XXXX XXXX |
Before you trash all your old CRC based designs, be advised that there is a trade-off associated with the Golay code’s error correction ability. If the code is used merely to detect errors, it can find a maximum 6 of them in any 24-bit codeword. However, if correction is performed, only three bits are correctable. Thus, we trade identifiable errors for correctability. As the code is used in an application, situations may demand changing the correction/detection methods to suit. Keep this trade-off in mind as you examine the performance of the Golay code and the requirements of your application.
Let’s look at the error trapping ability of the code. If error correction is not attempted, these are the error-detection-only properties, per 24-bit extended Golay codeword:
- 100% of one- to six-bit errors detected, any pattern
- 100% of odd bit-errors detected, any pattern
- 99.988% of other errors detected
Using the error correction facilities of the code, these are the data reliability rates:
- 100% of one- to three-bit errors corrected, any pattern
- 100% of four-bit errors detected, any pattern
- 100% of odd numbers of bit errors detected, any pattern
- 0.24% of other errors corrected (1/4096)
The parity bit of the extended Golay [24,12] code augments its error corrective properties, allowing all combinations of 4 bit errors to be detected, but not corrected.
Error correction is obviously no panacea and does carry a penalty. Let me explain why. When a codeword is being corrected, the correction algorithm looks for the closest matching codeword. For example, say codeword E86555h is transmitted (data=555h, checkbits=E86h), but four bit errors occur, corrupting the codeword to E86476h. When we feed this codeword into the correction function, it returns 68E4E6h as the closest matching codeword, not E86555h. The receiver can use the parity bit to detect this error, but higher even numbers of errors it cannot detect. This is called an uncorrectable error, and illustrates the fact that every correction algorithm has a bit- error-rate (BER) limit, beyond which it cannot compensate. Fortunately, you may enable the correction facilities of the given Golay C routines according to your needs.
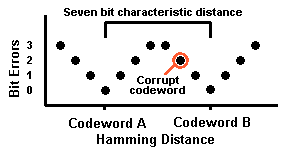
Simplified illustration of Golay [23,12] error correction.
Now for some mathematical curiosities. Among error correction codes, there is a class known as perfect codes. Briefly, perfect codes are defined as those where each of the invalid codewords, when pumped through the correction process, will be transformed into a valid codeword. There are no orphan uncorrectable information vectors. Included as perfect codes are the Hamming codes, a one-bit correction scheme, and the binary and ternary Golay codes. The Golay codes are the only nontrivial multiple error correcting perfect codes that exist3.
The perfect quality of the Golay code makes it an object of beauty in the eyes of mathematicians, especially when this property is expressed in terms of the optimum packing of spheres into a region of space4. However, the perfection of a code is not necessarily of concern to communications engineers.
The Golay codeword has some very interesting properties:
- Cyclic Invariance. If you take a 23-bit Golay codeword and cyclically shift it by any number of bits, the result is also a valid Golay codeword.
- Inversion. If you take a 23-bit Golay codeword and invert it, the result is also a valid Golay codeword.
- Minimum Hamming Distance. The distance between any two Golay [23,12] codewords is always seven or more bits. The distance between any two Golay [24,12] codewords is always eight or more bits.
- Error Correction. The correction algorithm can detect and correct up to three bit errors per codeword.
Let’s examine some practical aspects of the code.
What’s The Use?
The Golay code is obviously not able to encode a large amount of data in one codeword. Twelve bits is the maximum allowed per 23 or 24 bit codeword. So what is its use? Well, one advantage to error correction is the elimination of communications retries which can bog down a noisy channel. In some cases, the overhead associated with a resend request is much greater than the length of a data packet. For example, to send a data packet on a half duplex or simplex radio system, the microprocessor must turn on the transmitter and wait for it come up to full power, typically up to 100ms. The originating station must incur the same pre- transmit delay when resending its data. Even if all goes well, there is 200ms of wasted time involved in a resend request. At 1200 bits per second, 200ms represents 240 bits of data, a reasonable message length in some systems. And if the radio channel is busy with other traffic, the delays can be longer. The Golay code can reduce the number of retransmission events by allowing the receiving end to correct some errors in the received data, decreasing the probability that the channel will get overloaded.
In other situations, there may be no resend request possible, say, with a one-way RF, infrared or ultrasonic data link. The Golay code allows such systems to increase the probability of one-way, error-free, reception.
Some communications channels are more prone than others to burst errors, where many consecutive data bits are corrupted. The Golay code is not alone able to correct bursts of errors over three bits long in a single codeword. However, when augmented with a technique called bit interleaving, the Golay code’s small, modular format allows the correction of large burst errors, as we will see later. The unmodified Golay code really shines in applications prone to random bit errors though, and it tolerates a disgusting (3 bit errors)/(24 bits per codeword) = 12.5% bit error rate without data retransmissions.
Of course, a disadvantage of the extended Golay code is that you must transmit as many check bits as data bits. Maybe you are asking, why not just send the data twice, without check bits? The answer is that no error correction is possible in such a system. How would you know which of two different messages, if not both, were corrupt? The Golay code allows error correction in exchange for the data-doubling price.
Golay Code Implementation – Encoding
The Golay code is encoded just like the CRC, using modulo-2 division. However, there are only 12 information bits per codeword, so you must break your data down into 12-bit chunks and encode each as one codeword. The characteristic polynomials for the Golay code are:
- X11 + X9 + X7 + X6 + X5 + X + 1, coefficients AE3h.
- X11 + X10 + X6 + X5 + X4 + X2 + 1, coefficients C75h.
Yes, there are two. You only need use one of them because they both have the same properties as mentioned above, though they generate differing checkbits. Pull a coin and choose a polynomial! We will use the coefficients of the X terms of the first polynomial, AE3h. Note that AE3h is the bit-reversed version of C75h, a byproduct of the code’s cyclic nature.
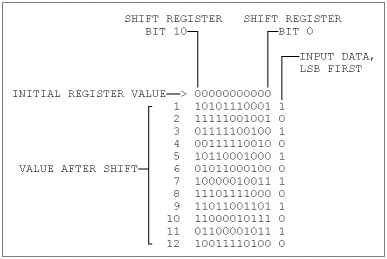
An example worked out by hand illustrates the modulo-2 division process. Remember that in modulo-2 division we exclusive-OR instead of subtract. The data we wish to encode is 555h. To generate the 11 check bits, append 11 zeros onto the bit-reversed data (LSB first) and perform the division below.
Golay
polynomial info bits zero fill
|----------| |----------||---------|
________________________
101011100011 )10101010101000000000000
101011100011
------------ <---------- Exclusive-OR
100100100000
101011100011
------------
111100001100
101011100011
------------
101111011110
101011100011
------------
100111101000
101011100011
------------
01100001011 <-- checkbits
We only care about the bit-reversed remainder from the division, 11010000110 = 686h, and so do not even write down the quotient. Putting the codeword together for transmission, we get 686555h. A parity bit could be added to the codeword to make an extended Golay code. Of course, you can scramble the bits around in any order for transmission, just as long as they are reassembled correctly before decoding. Grouping the checkbits and information bits together as we have done here is called systematic encoding.
The encoding algorithm is shown below. Long integers are used to conveniently store one codeword.
#define POLY 0xAE3 /* or use the other polynomial, 0xC75 */
unsigned long golay(unsigned long cw)
/* This function calculates [23,12] Golay codewords.
The format of the returned longint is
[checkbits(11),data(12)]. */
{
int i;
unsigned long c;
cw&=0xfffl;
c=cw; /* save original codeword */
for (i=1; i<=12; i++) /* examine each data bit */
{
if (cw & 1) /* test data bit */
cw^=POLY; /* XOR polynomial */
cw>>=1; /* shift intermediate result */
}
return((cw<<12)|c); /* assemble codeword */
}
The routine parity() adds the parity bit to complete the extended codeword. It is shown below.
int parity(unsigned long cw)
/* This function checks the overall parity of codeword cw.
If parity is even, 0 is returned, else 1. */
{
unsigned char p;
/* XOR the bytes of the codeword */
p=*(unsigned char*)&cw;
p^=*((unsigned char*)&cw+1);
p^=*((unsigned char*)&cw+2);
/* XOR the halves of the intermediate result */
p=p ^ (p>>4);
p=p ^ (p>>2);
p=p ^ (p>>1);
/* return the parity result */
return(p & 1);
}
Golay Code Implementation – Detecting Errors
Detection of errors in a codeword is easy. First, we use the overall parity bit to check for odd numbers of errors, possibly failing the codeword on that basis. If parity is correct, we compute the 23-bit syndrome of the codeword and check for zero. The syndrome is the remainder left after the codeword is divided by the generating polynomial, modulo-2. If the codeword is a valid Golay codeword, the syndrome is zero, else non-zero. The computation below shows a sample calculation using the previously constructed codeword, 686555h, bit reversed for the division process.
________________________
101011100011 )10101010101001100001011
101011100011
------------
100100101100
101011100011
------------
111100111100
101011100011
------------
101110111111
101011100011
------------
101011100011
101011100011
------------
000000000000 <-- syndrome = 0
The routine in the next listing does the same sort of calculation. You could use a table of intermediate results to speed the process.
unsigned long syndrome(unsigned long cw)
/* This function calculates and returns the syndrome
of a [23,12] Golay codeword. */
{
int i;
cw&=0x7fffffl;
for (i=1; i<=12; i++) /* examine each data bit */
{
if (cw & 1) /* test data bit */
cw^=POLY; /* XOR polynomial */
cw>>=1; /* shift intermediate result */
}
return(cw<<12); /* value pairs with upper bits of cw */
}
These routines are all you need to implement a Golay error detection scheme. As above, you can detect up to 6 bit errors per codeword and, with the parity bit, all odd numbers of errors.
Implementation – Correcting Errors
Cue the smoke and mirrors; error correction is not so trivial. It relies on the cyclic properties of Golay codewords in a scheme called systematic search decoding2. There are other methods of Golay error correction listed in the references, though I have found this one easy to implement in software. This is a ‘nearest neighbor decoder’, because it determines which Golay codeword is closest in terms of Hamming distance.
Here is a sketch of the systematic search algorithm.
1. Compute the syndrome of the codeword. If zero, no errors exist so go to step 5. If a trial bit has been toggled, go to step 2a, else 2.
2. If the syndrome has a weight of three or less, the syndrome matches the error pattern bit-for-bit, and can be used to exclusive-OR the errors out of the codeword; if so, remove the errors and go to step 5, else proceed to step 3.
2a. If the syndrome has a weight of one or two, the syndrome matches the error pattern bit-for-bit, and can be used to exclusive-OR the errors out of the codeword; if so, remove the errors and go to step 5, else proceed.
3. Toggle a trial bit in the codeword in an effort to eliminate one bit error. Restore any previously toggled trial bit. If all 23 bits have been toggled and tried once, go to step 4; else go to step 2a.
4. Rotate the codeword cyclically left by one bit. Go to step 1.
5. Rotate the codeword right to its original position, if needed.
The idea is to fiddle with the codeword until the syndrome has a weight of three or less, in which case we can exclusive-OR the syndrome with the codeword to negate the errors. However, if a trial bit has been toggled, we might have introduced an error (making a total of 4), so the threshold for exclusive-ORing the errors away in step 2a must be reduced by one for safety, to two or less.
We are relying on the perfect nature of the Golay code for a terminating condition of the systematic search algorithm. Normally, we would test in step 4 to see if all 23 shifts of the codeword had already been tried, but since the Golay code is perfect, we know that each 23-bit value maps to exactly one correct Golay codeword and the algorithm will terminate. (However, since the Golay code is perfect but programmers are not, I test to guard against infinite loops. Paranoia is my friend.)
Bring Out The Source Code!
Now to the good stuff, the source code that makes the system work for you.
The rotations and trial bit bookkeeping make for a nontrivial looking routine for Golay error correction, correct(), shown below with its support routines. These routines are written for simplicity. You can tighten them up for optimum performance on your favorite scream machine.
int weight(unsigned long cw)
/* This function calculates the weight of
23 bit codeword cw. */
{
int bits,k;
/* nibble weight table */
const char wgt[16] = {0,1,1,2,1,2,2,3,1,2,2,3,2,3,3,4};
bits=0; /* bit counter */
k=0;
/* do all bits, six nibbles max */
while ((k<6) && (cw))
{
bits=bits+wgt[cw & 0xf];
cw>>=4;
k++;
}
return(bits);
}
unsigned long rotate_left(unsigned long cw, int n)
/* This function rotates 23 bit codeword cw left by n bits. */
{
int i;
if (n != 0)
{
for (i=1; i<=n; i++)
{
if ((cw & 0x400000l) != 0)
cw=(cw << 1) | 1;
else
cw<<=1;
}
}
return(cw & 0x7fffffl);
}
unsigned long rotate_right(unsigned long cw, int n)
/* This function rotates 23 bit codeword cw right by n bits. */
{
int i;
if (n != 0)
{
for (i=1; i<=n; i++)
{
if ((cw & 1) != 0)
cw=(cw >> 1) | 0x400000l;
else
cw>>=1;
}
}
return(cw & 0x7fffffl);
}
unsigned long correct(unsigned long cw, int *errs)
/* This function corrects Golay [23,12] codeword cw, returning the
corrected codeword. This function will produce the corrected codeword
for three or fewer errors. It will produce some other valid Golay
codeword for four or more errors, possibly not the intended
one. *errs is set to the number of bit errors corrected. */
{
unsigned char
w; /* current syndrome limit weight, 2 or 3 */
unsigned long
mask; /* mask for bit flipping */
int
i,j; /* index */
unsigned long
s, /* calculated syndrome */
cwsaver; /* saves initial value of cw */
cwsaver=cw; /* save */
*errs=0;
w=3; /* initial syndrome weight threshold */
j=-1; /* -1 = no trial bit flipping on first pass */
mask=1;
while (j<23) /* flip each trial bit */
{
if (j != -1) /* toggle a trial bit */
{
if (j>0) /* restore last trial bit */
{
cw=cwsaver ^ mask;
mask+=mask; /* point to next bit */
}
cw=cwsaver ^ mask; /* flip next trial bit */
w=2; /* lower the threshold while bit diddling */
}
s=syndrome(cw); /* look for errors */
if (s) /* errors exist */
{
for (i=0; i<23; i++) /* check syndrome of each cyclic shift */
{
if ((*errs=weight(s)) <= w) /* syndrome matches error pattern */
{
cw=cw ^ s; /* remove errors */
cw=rotate_right(cw,i); /* unrotate data */
if (j >= 0) /* count toggled bit (per Steve Duncan) */
*errs=*errs+1;
return(s=cw);
}
else
{
cw=rotate_left(cw,1); /* rotate to next pattern */
s=syndrome(cw); /* calc new syndrome */
}
}
j++; /* toggle next trial bit */
}
else
return(cw); /* return corrected codeword */
}
return(cwsaver); /* return original if no corrections */
} /* correct */
The correct() function returns the nearest matching Golay codeword. Note that this may not be the codeword you expect, if there are more than three bit errors, because the received, corrupted codeword may be closer in terms of Hamming distance to a different Golay codeword. (Thanks to Steve Duncan for the error correction correction (!), above.)
While I’m loading your shopping cart with source code, below appears decode(), a function for either detecting or correcting errors in Golay [24,12] codewords, returning the corrected codeword and error detection status.
int decode(int correct_mode, int *errs, unsigned long *cw)
/* This function decodes codeword *cw in one of two modes. If correct_mode
is nonzero, error correction is attempted, with *errs set to the number of
bits corrected, and returning 0 if no errors exist, or 1 if parity errors
exist. If correct_mode is zero, error detection is performed on *cw,
returning 0 if no errors exist, 1 if an overall parity error exists, and
2 if a codeword error exists. */
{
unsigned long parity_bit;
if (correct_mode) /* correct errors */
{
parity_bit=*cw & 0x800000l; /* save parity bit */
*cw&=~0x800000l; /* remove parity bit for correction */
*cw=correct(*cw, errs); /* correct up to three bits */
*cw|=parity_bit; /* restore parity bit */
/* check for 4 bit errors */
if (parity(*cw)) /* odd parity is an error */
return(1);
return(0); /* no errors */
}
else /* detect errors only */
{
*errs=0;
if (parity(*cw)) /* odd parity is an error */
{
*errs=1;
return(1);
}
if (syndrome(*cw))
{
*errs=1;
return(2);
}
else
return(0); /* no errors */
}
} /* decode */
The parity bit in the extended Golay code is used as a final check on the integrity of the corrected codeword. If the received codeword has the right parity, the codeword is accepted, else it is rejected. The overall parity bit is used to trap the occurrence of odd numbers of errors and four-bit-error laden codewords.
Why does the overall parity bit help to trap four bit errors? This is explained by the fact that the correction algorithm introduces three additional bit changes to get to the nearest codeword, which is seven bits distant from the original, noncorrupt codeword. Assume we have four bit errors in a codeword. The four bit errors, plus three additional changed bits makes seven bit changes total, and that changes the codeword’s parity. So the overall parity bit helps to trap four bit errors, but only after correction has been attempted.
If one of the four errors is in the parity bit, the 23-bit codeword will be corrected properly, but must be discarded because the total parity is wrong and the receiver will not know exactly which bits were corrupted. For the interested few, this will occur in
of cases of four bit errors, where C(n,r) is the number of combinations of n things taken r at a time.
Back To Reality
In practice, I have used the Golay code on radio channels and telephone lines, and have found it to be robust. Practically, one cannot rely on the error correction facilities alone, if there is a two-way communication link. Rather, I use the Golay code to reduce the incidence of message resends. Messages are always checked for framing errors and other problems which are specific to the information transmitted and the message context.
A frailty of the Golay code is its inability to detect large bursts of bit errors. However, a technique called bit interleaving can remedy the situation. Assume we have a block of 48 bits to transmit, two codewords. An error of 4 consecutive bits will corrupt a Golay data packet and elicit a retransmission. However, if we transmit the 48 bits not in 2 sequential Golay codewords, but in a scrambled order, burst errors will be distributed over both codewords when the bits are unscrambled.
Original codewords:
111111111111111111111111 000000000000000000000000
Interleaved codewords:
101010101010101010101010 010101010101010101010101
After a six bit burst error:
101010101001010110101010 010101010101010101010101
xxxxxx
6 bit-errors
After de-interleave:
111110001111111111111111 000001110000000000000000
xxx xxx
three bit-errors three bit-errors
(correctable) (correctable)
The two resulting codewords are correctable, whereas a six-bit burst error in the original data would not have been. In general, the more data you interleave, the longer the burst of errors the message can withstand. The correctable burst size, in bits, is three times the number of codewords interleaved.
The penalty is the reception delay incurred between the first and last bit of any one codeword. Using this method, it is theoretically possible to extend the 3/24=12.5% burst error correction capability of the Golay [23,12] code to arbitrarily long blocks of data. Imagine sending a 100-codeword, 2400 bit message and correcting a burst error of 300 consecutive bits!
You may have noticed that the codewords used in the above examples are 000000h and FFFFFFh. These are valid Golay codewords. This alerts us to a possible communications failure mode: the stuck bit. If the hardware were to fail in mid-message, it could emit a default 1 or 0, depending on its configuration and the data format. This could be disastrous if undetected because the dead circuit would be interpreted as sending consecutive, valid Golay codewords.
Happily, we can modify the Golay checkbits slightly, as is often done when using CRCs, by inverting one or more of them before transmission, and reinverting the same bits before decoding at the receiver. This way, 000000h and FFFFFFh are not valid Golay codewords, and the chances of a stuck data line mimicing good data are greatly reduced. In fact it is always good practice to structure your communications protocol so that a continuous 0 or 1 block of data cannot be misconstrued as valid information.
By the way, do not ignore the information that spins off of the correction process: The number of errors corrected in each codeword. This is valuable information about the BER on the communications channel, useful for judging its quality. Say that you have a data system running over the telephone network in a remote area and these lines are not the best quality, degrading some with the weather. (This is not a contrived example. Some Mom ‘n Pop telcos run with twine and tin cans.) It would be nice to optimize the data rate based on the current condition of the lines.
Counting corrected bit errors is one way to do this. As the error rate (corrected bits / total bits) passes a critical value, the data rate can be cut, with the cooperation of transmitter and receiver, of course. When the sun comes out, the data rate can be increased as the BER goes down to acceptable levels. (Note that this technique has a BER measurement ceiling of 12.5% because every corrupt codeword will have at most three correctable errors.)
Shift Register Golay Encoders
I am sure that some readers are hardware types, wondering if the Golay code can be easily implemented in hardware. The references to this article describe various circuits suitable to the task of decoding — I mean suitable as a function of your personal Boolean logic overload level. The circuits are not trivial by any means, though the relatively small number of 4096 Golay codewords suggests that ROM based decoders may be economical. The decoder would easily fit in a small FPGA, too.
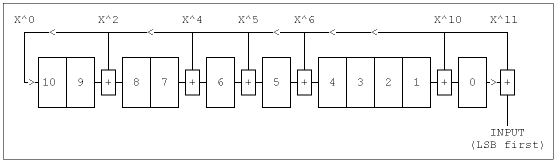
The shift register implementations of the two Golay checkbit generators are simple, and are shown in Figures 1 and 2.
________________________
110001110101 )10101010101000000000000
110001110101
------------
110110111110
110001110101
------------
111001011000
110001110101
------------
100010110100
110001110101
------------
100110000010
110001110101
------------
101111101110
110001110101
------------
111100110110
110001110101
------------
110100001100
110001110101
------------
00101111001
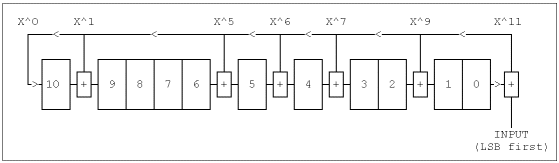
Figure 2. Golay checkbit generator and example for polynomial X11 + X10 + X6 + X5 + X4 + X2 + 1.
As before, either circuit produces valid Golay checkbits. Also shown is a sample calculation. The final register value in the top example is 11010000110, which we reverse and compare with the result of a previous hand calculation, finding agreement. This circuit is equivalent to that calculation with input data of 555h. The final register value of Figure 1 is 10011110100, which agrees with the accompanying modulo-2 division remainder, when reversed. Also notice that, like the two polynomials, the shift register circuits are mirror images of each other, suggesting that some more gating could make one bidirectional shift register encode either polynomial.
Conclusion
Of course, there are other error correcting codes, but it is generally agreed in the literature that they are more difficult to correct than the Golay code, though the Hamming codes are easier. In general, the more capable the code, the more processor power it takes to decode. The Golay code could be used in even the smallest microcontrollers, such as the PIC series and 68HC05.
As a parting imperative, do your homework before choosing this or any other error detection/correction code. There are some important ideas that we did not discuss here, such as coding gain. This is an expression of the improvement in performance of the coded channel over the uncoded channel. Each code has a different coding gain for various channel noise conditions.
You should also examine the references for matrix methods of encoding and decoding the Golay and other codes. And let me recommend the routine golay_test(), below. It does tests to verify the operation of your encoding and decoding routines by letting you induce a selectable number of errors in a test codeword on which correction is attempted. Always test your versions of these routines thoroughly before deploying; it is easy to slip up on a loop index and get a data-dependent error detector or corrector, which is certain to ruin a couple of nights’ sleep.
void golay_test(void)
/* This function tests the Golay routines for detection and correction
of various patterns of error_limit bit errors. The error_mask cycles
over all possible values, and error_limit selects the maximum number
of induced errors. */
{
unsigned long
error_mask, /* bitwise mask for inducing errors */
trashed_codeword, /* the codeword for trial correction */
virgin_codeword; /* the original codeword without errors */
unsigned char
pass=1, /* assume test passes */
error_limit=3; /* select number of induced bit errors here */
int
error_count; /* receives number of errors corrected */
virgin_codeword=golay(0x555); /* make a test codeword */
if (parity(virgin_codeword))
virgin_codeword^=0x800000l;
for (error_mask=0; error_mask<0x800000l; error_mask++)
{
/* filter the mask for the selected number of bit errors */
if (weight(error_mask) <= error_limit) /* you can make this faster! */
{
trashed_codeword=virgin_codeword ^ error_mask; /* induce bit errors */
decode(1,&error_count,&trashed_codeword); /* try to correct bit errors */
if (trashed_codeword ^ virgin_codeword)
{
printf("Unable to correct %d errors induced with error mask = 0x%lX\n",
weight(error_mask),error_mask);
pass=0;
}
if (kbhit()) /* look for user input */
{
if (getch() == 27) return; /* escape exits */
/* other key prints status */
printf("Current test count = %ld of %ld\n",error_mask,0x800000l);
}
}
}
printf("Golay test %s!\n",pass?"PASSED":"FAILED");
}
References
1. Golay, Marcel J.E., “Notes on Digital Coding”, Proceedings of the IRE, Vol. 37, June, 1949, pp. 657.
2. Lin, Shu, An Introduction to Error Correcting Codes. Englewood Cliffs, N.J., Prentice-Hall, 1970, pp. 101-106.
3. MacWilliams, Sloane, The Theory of Error Correcting Codes. Amsterdam, North Holland Publishing Co., 1977, pp. 64-65, 482, 634-635.
4. Pless, Vera, Introduction to the Theory of Error Correcting Codes. John Wiley & Sons, 1982, pp. 1-13.
5. Shannon, C.E., “A Mathematical Theory of Communication”, Bell System Technical Journal, Vol. 27, July, 1948, pp. 379-423; October, 1948, pp. 623-656.
Author Biography
Hank Wallace is the owner of Atlantic Quality Design, Inc., a consulting firm located in Fincastle, Virginia. He has experience in many areas of embedded software and hardware development, and system design. See www.aqdi.com for more information.
